Calculus III completes a typical Calculus series and covers multivariable calculus. It assumes a good knowledge of one-variable calculus as well as the fundamentals of linear algebra. This course is intended for Math majors and is focused on theory and proofs.
Learn more about this Content Pack here.
Introductory Statistics follows scope and sequence requirements of a one-semester introduction to statistics course and is geared toward students majoring in fields other than math or engineering. The course assumes some knowledge of intermediate algebra and focuses on statistics application over theory.
Learn more about this Content Pack here.
Linear Algebra covers most of a typical first year Linear Algebra course with a focus on applications in Sciences. This course explores systems of linear equations, matrix algebra, determinants, and introduces vector spaces and their applications.
Learn more about this Content Pack here.
This is is a fist year Algebra course centered on proof, the defining property of Mathematics. The course provides an introduction to the language of mathematics and proof techniques through a study of the basic algebraic systems of mathematics.
Learn more about this Content Pack here.
In this course students will learn the theory of rates of interest and discount; annuities and sinking funds with practical applications to mortgage and bond questions; yield rates.
Learn more about this Content Pack here.
This course is best suited as a Foundations of Mathematics course often taught in post-secondary institutions, covering four modules on Algebra and Geometry core principles. This course serves as an excellent prerequisite to first year college or university level Algebra and Geometry.
Learn more about this Content Pack here.
Undergraduate course that covers mechanics, sound, oscillations, and waves. This course emphasizes connections between theory and application, making physics concepts interesting and accessible to students while maintaining the mathematical rigour inherent in the subject. Frequent, strong examples focus on how to approach a problem, how to work with the equations, and how to check and generalize the result.
Learn more about this Content Pack here.
Precalculus is a comprehensive course that covers more ground than a typical one- or two-semester college-level precalculus course. The content is organized by clearly-defined learning objectives and includes worked examples that demonstrate problem-solving approaches in an accessible way.
Learn more about this Content Pack here.
This course in differential equations covers standard approaches to solving first order ordinary differential equations along with associated qualitative analyses, second order linear differential equations and systems of differential equations. Examples and applications are drawn from the sciences and engineering.
Learn more about this Content Pack here.
Students can learn about roughly a dozen problem techniques (such as, “draw a useful diagram”, “find a pattern”, and consider cases) and explicitly look at problem solving in a number of major topic areas (such as Number Theory, Counting, and Geometry).
Learn more about this Content Pack here.
This material highlights derivatives of polynomial, rational, exponential, logarithmic, trigonometric functions, integral calculus, real-world applications, vectors, lines, and planes.
Learn more about this Content Pack here.
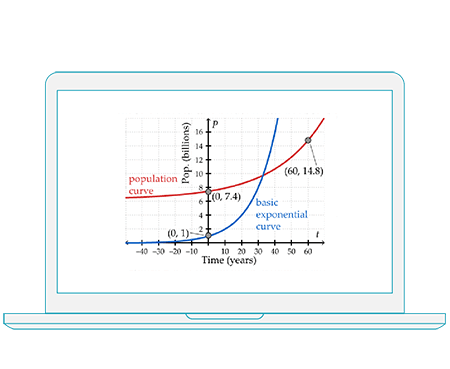
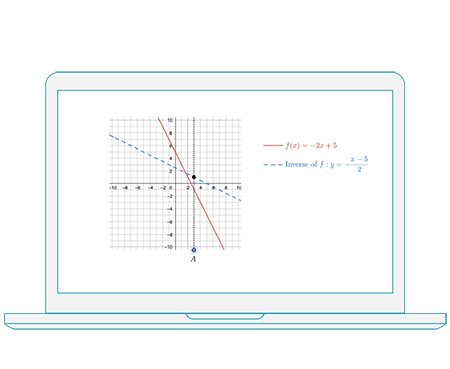
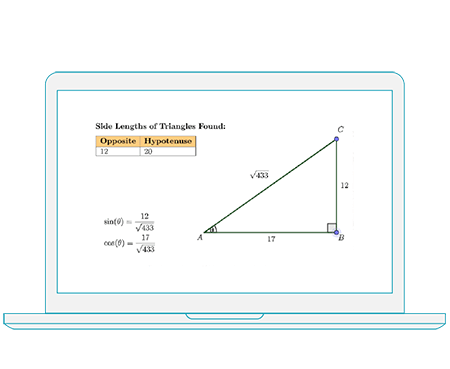
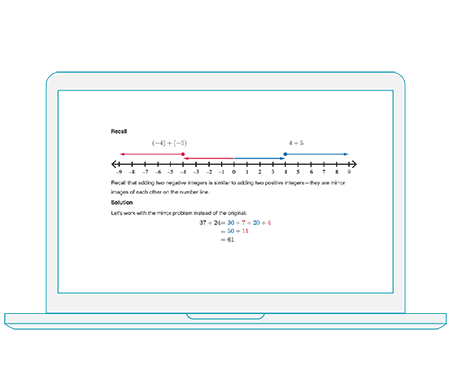
This course in differential and integral calculus begins with a review of functions, introduces limits and explores the derivative both from a limit-based and rule-based approach, covering elementary functions and applications. Integration is introduced from the perspective of anti-differentiation, followed by coverage of Riemann sums and the Fundamental Theorems, definite and indefinite integrals and solution techniques. Arc length, area and volume integrals and other applications are introduced. Series and convergence are explored, followed by an introduction to differential equations. Finally, parametric curves and polar coordinates, and the basics of multivariable calculus are presented. Examples are drawn from applications in the sciences.
Learn more about this Content Pack here.
This course is designed to support instructors who are teaching elements of Euclidean geometry, from properties of triangles and circles to applications. The material is designed around building problem solving and proof skills.
Learn more about this Content Pack here.
This course is designed to support instructors who are teaching elements of Euclidean geometry, from properties of triangles and circles to applications. The material is designed around building problem solving and proof skills.
Learn more about this Content Pack here.
This course extends students' experience with functions. Students can investigate the properties of polynomial, rational, exponential, logarithmic, trigonometric and radical functions; develop techniques for combining functions; broaden their understanding of rates of change; and develop facility in applying these concepts and skills.
Learn more about this Content Pack here.
Algebra and Trigonometry provides a comprehensive exploration of algebraic principles and meets scope and sequence requirements for a typical introductory algebra and trigonometry course. Algebra and Trigonometry offers a wealth of examples with detailed, conceptual explanations, building a strong foundation in the material before asking students to apply what they’ve learned.
Learn more about this Content Pack here.
Students will be presented with course material that encompasses exponential and sinusoidal functions, properties, transformations, and applications.
Learn more about this Content Pack here.
Students will experience a firm foundation in functions while exploring function notation, domain and range, transformations of functions, inverses of functions, inequalities, absolute values, and reciprocals.
Learn more about this Content Pack here.
Course material that is comprised of lessons relating to linear and non-linear relations, solving linear equations and linear systems, analytic geometry, and statistics.
Learn more about this Content Pack here.
This content pack includes course modules for students that cover the Pythagorean theorem, measurement of 2D figures and 3D solids, optimization, geometric relationships, triangle trigonometry, angles in standard position, and trigonometric identities.
Learn more about this Content Pack here.
This course material provides students with lessons to learn about exponent laws, manipulating expressions including polynomials, radical and rational expressions, and investigating prime factorization.
Learn more about this Content Pack here.
Pre-built lessons that cover negative numbers and fractions, basic algebra through patterning, proportional reasoning, and other topics, polygons, circles, and triangles.
Learn more about this Content Pack here.
These lessons cover graphs and tables, standard, factored and vertex forms, algebra of quadratic relations, quadratic equations, and intersections of lines and parabolas.
Learn more about this Content Pack here.
Lesson material that spans arithmetic and geometric sequences, financial applications including simple interest, compound interest, and annuities.
Learn more about this Content Pack here.
Premium packs are full courses that can be purchased alongside the Starter Content Bundle. As with our starter content, all premium courses are designed specifically for Möbius, and can be edited or modified by instructors to suit your class perfectly.
This course uses the unit circle approach to learning trigonometry as this approach fits much better with the concept of functions. In addition, this approach allows most topics in trigonometry to be built upon the unit circle.
Learn more about this Content Pack here.
An introductory undergraduate course in differential and integral calculus composed of five units Limits, Derivatives, Applications of Derivatives, Integrals, and Applications of Integrals.
Learn more about this Content Pack here.